CyberApocalypse_2023 - Crypto - SmallSteps (Very easy)

Crypto - SmallSteps (Very easy)

This is a crypto challenge using RSA algorithm.

The solver.py code in this challenge

from Crypto.Util.number import getPrime, bytes_to_long

FLAG = b"HTB{???????????????}"
assert len(FLAG) == 20


class RSA:

    def __init__(self):
        self.q = getPrime(256)
        self.p = getPrime(256)
        self.n = self.q * self.p
        self.e = 3

    def encrypt(self, plaintext):
        plaintext = bytes_to_long(plaintext)
        return pow(plaintext, self.e, self.n)


def menu():
    print('[E]ncrypt the flag.')
    print('[A]bort training.\n')
    return input('> ').upper()[0]


def main():
    print('This is the second level of training.\n')
    while True:
        rsa = RSA()
        choice = menu()

        if choice == 'E':
            encrypted_flag = rsa.encrypt(FLAG)
            print(f'\nThe public key is:\n\nN: {rsa.n}\ne: {rsa.e}\n')
            print(f'The encrypted flag is: {encrypted_flag}\n')
        elif choice == 'A':
            print('\nGoodbye\n')
            exit(-1)
        else:
            print('\nInvalid choice!\n')
            exit(-1)


if __name__ == '__main__':
    main()

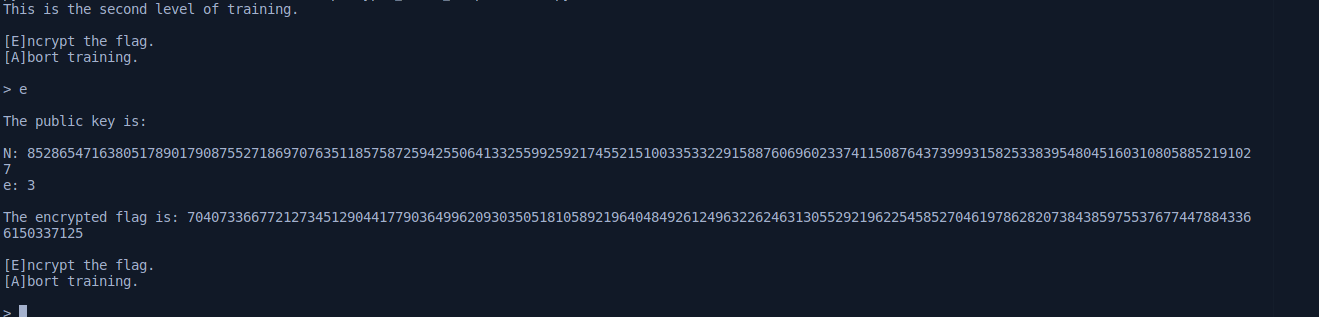
Output of the code

Enter ‘e’ & you will get the following value: n, e & the cipher text

There is potential security flaw with using a small exponent (e=3) and a short message m.

Solving the challenge using Python code

import sys
n=6440820796664237152257805121902653527479878427879627941066487312258833640115686093188400302219595334711407038182954978084471026764022347102404900173244213
n=hex(n)
e=3
cipher=70407336670535933819674104208890254240063781538460394662998902860952366439176467447947737680952277637330523818962104685553250402512989897886053
import gmpy2
 
#f = open('cipher','rb')
#cipher = int(f.read().encode('hex'),16)
with gmpy2.local_context(gmpy2.context(), precision=800) as ctx:
 ctx.precision += 800
 root = gmpy2.cbrt(cipher)

try:
	print(str('%x' % + int(root)).decode('hex'))
except AttributeError:
	print(bytes.fromhex(str('%x' % + int(root))).decode('utf-8'))

HTB flag

HTB{5ma1l_E-xp0n3nt}